#

1-практикa

  1. Главная
  2. Список практики
  3. 1-практикa

Тема практической работы: «Оценка объема информации, используя формулы Хартли и Шеннона».

Цель: обучение переводу информации из одной единицы измерения в другую и вычислению количества информации с помощью формул Хартли и Шеннона.

Оборудование: интерактивная доска для демонстрации компьютера учителя.

Ход занятия:

Актуализация знаний

  1. Что такое информация?
  2. Какие существуют формы хранения информации? 
  3. Перечислите возможные источники информации.

Изложение нового материала

На данном уроке рассмотрим единицы измерения информации, формулы Хартли и Шеннона, и способы их применения. 

Измерение информации – это процесс получения численной характеристики, которая должна обладать единицей измерения. Чаще всего измеряют количество места, которое требуется для хранения той или иной информации. В таком случае можно выделить следующие единицы измерения информации: биты, байты, килобайты, мегабайты, гигобайты и т.д. При этом наименьшей единицей измерения информации являются биты и работает следующая таблица перевода (представлены самые часто используемые в заданиях единицы измерения):

1 байт  = 8 бит = 23 бит,

1 килобайт (1 Кбайт)  = 1024 байт = 210 байт,

1 мегабайт (1 Мбайт)  = 1024 Кбайт = 210 Кбайт,

1 гигабайт (1 Гбайт) = 1024 Мбайт = 210 Мбайт.

Выполним задания, связанные с переводом из одной единицы измерения информации в другую.

Задание 1. Сколько битов составляют 20 байтов?

Решение

Т.к. в 1 байте находится 8 битов информации, то в 20 байтах находится в 8 раз больше битов. Поэтому нужно умножить 20 на 8. В результате получим:


Ответ: 160 битов

Задание 2. Сколько байтов содержится в 1293010 битах информации?

Решение

Чтобы перевести информацию, выраженную в битах, в байты, необходимо разделить представленную в задании информацию на 8. В результате получим:

A black numbers on a white backgroundDescription automatically generated

Ответ: 161626,25 байтов

Задание 3. Сколько байтов содержится в 2 Гбайтах информации?

Решение

Чтобы перевести информацию из гигабайт в байты необходимо сначала перевести информацию в мегабайты, затем в в килобайты, а только потом в биты. 

Для удобства понимания запишем решение по действиям: 

  1. Чтобы перевести из гигабайтов в мегабайты необходимо исходное количество гигабайт умножить на 1024 Мбайт. При этом удобнее представить 1024 как 210. В результате получим:
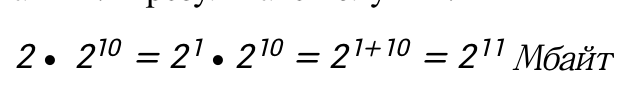
image


 

  1. Чтобы перевести из мегабайтов в килобайты необходимо полученное количество мегабайт умножить на 210 Кбайт. В результате получим:


  1. Чтобы перевести из килобайтов в байты необходимо полученное количество килобайт умножить на 210 байт. В результате получим:


Ответ: 231 байтов

Теперь узнаем, что собой представляет формула Хартли и каким образом с ее помощью можно измерить количество информации.

Формула Хартли – это математическая формула, которая применяется для оценки количества информации в сообщении на основе количества символов в алфавите и количества символов в конкретном сообщении.

Формула Хартли выглядит следующим образом:

             

A black text on a white backgroundDescription automatically generated                                    (1)

где

 – количество информации в битах,

N – количество символов в алфавите.

Также данную формулу можно преобразовать следующим образом:

                  

A black and white math symbolDescription automatically generated                                   (2)

Следует запомнить, что формулу Хартли следует применять в том случае, когда наступление каждого из событий является равновероятным. Можно сказать, что возможность наступления какого-либо события из конкретного перечня событий является одинаковым.

Выполним задания, связанные с применением формулы Хартли.

Задание 1. В непрозрачном мешке находится 64 пронумерованных шара. Сколько информации содержится в сообщении о первом вытащенном шаре? 

Решение

Количество информации в сообщении – это . Получается, что вероятность события вытащить шар под любым номером будет одинаковой, т.к. у нас 64 разных шара. Получается, что мы можем использовать формулу Хартли. Подставим в формулу (1) известную информацию и вычислим количество бит полученной информации:


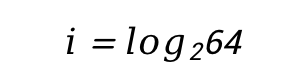
A black text on a white backgroundDescription automatically generated

Для понимания процесса вычисления логарифма нужно вспомнить, из каких компонентов он состоит:

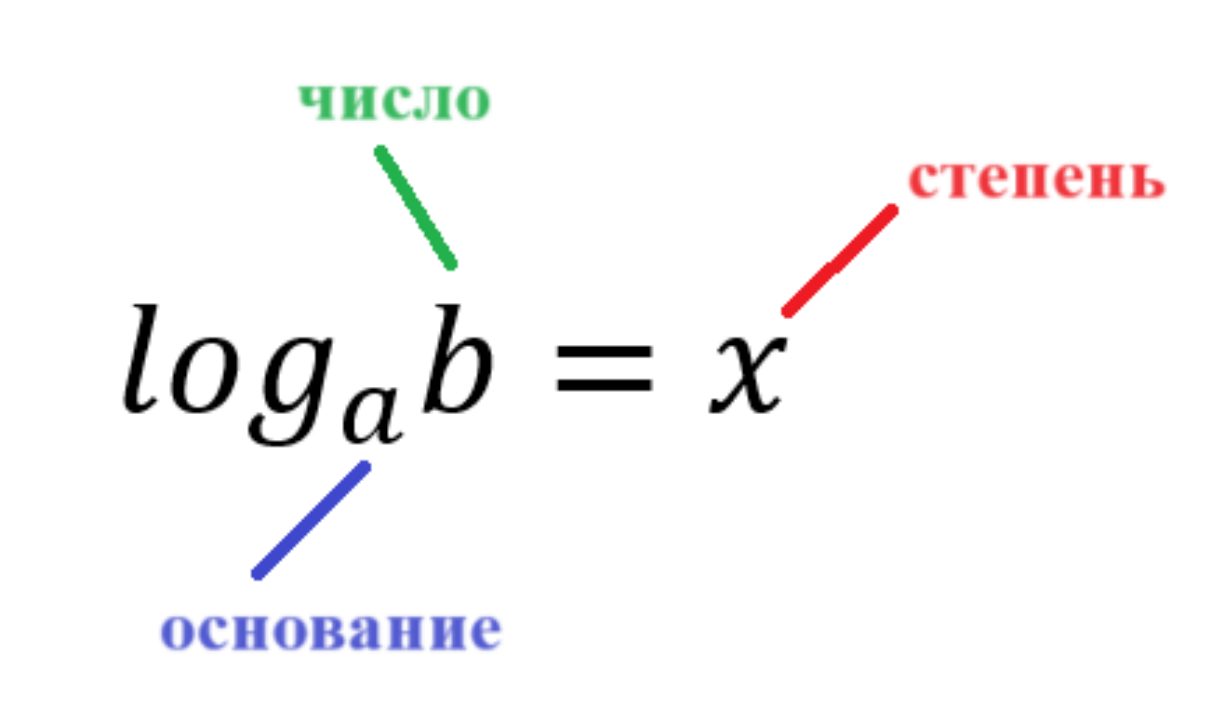
Изображение выглядит как текст, Шрифт, линия, числоАвтоматически созданное описание

Читается “в какую степень нужно возвести основание, чтобы получить число”

Примеры вычисления логарифмов:

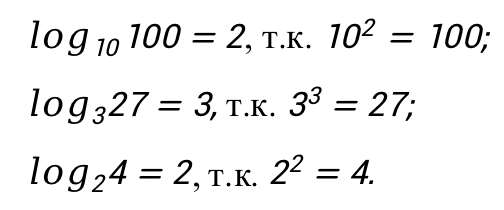
A math equations and equationsDescription automatically generated with medium confidence

Теперь вернемся к задаче и решим ее.



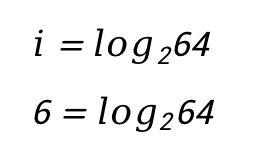
A math equations and symbolsDescription automatically generated with medium confidence

Ответ: 6 битов

Задача 2. При вытаскивании из корзины произвольного шара было получено 8 битов информации. Сколько чисел содержится в данном алфавите?

Решение

Количество чисел в алфавите – это N. Для вычисления используем формулу (2):

,

.

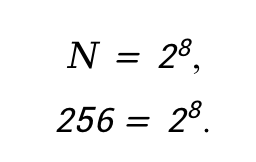
A number and equation with numbersDescription automatically generated with medium confidence

Количество чисел в алфавите не имеет единиц измерения, поэтому в ответ запишем только число.

Ответ: 256

Формула Шеннона – это математическая формула, которая применяется для вычисления количества информации в ситуациях, когда вероятности наступления событий, участвующих в необходимом информационном процессе, являются разными.

Формула Шеннона выглядит следующим образом:


 

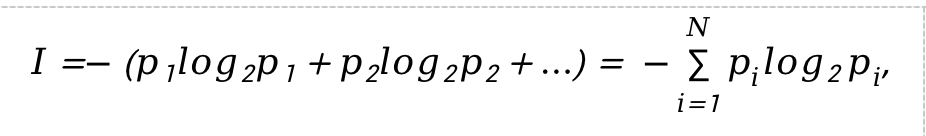
A black text with black lettersDescription automatically generated with medium confidence

(3)

где

– среднее количество информации,

N – количество возможных событий,

 – вероятность i-го события.

При этом количество информации для одного такого события равно:

    или                                   (4)

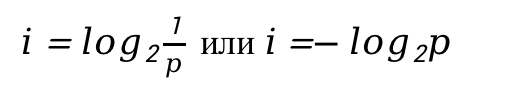
A black text on a white backgroundDescription automatically generated


где

 – вероятность наступления данного события.

Выполним задания, связанные с применением формулы Шеннона.

Задача 1. В группе студентов-программистов обучается 24 человека. За экзамен по дисциплине «Элементы высшей математики» были получены следующие отметки: 3 отметки «2», 6 отметок «3», 12 отметок «4», 3 отметки «5». Определите, какое количество информации содержит сообщение об отметке любого студента данной группы.

Решение

Т.к. в группе студентами было получено разное количество двоек, троек, четверок и пятерок, то получается, что события получения разных отметок будут отличаться. В таком случае воспользуемся формулой Шеннона.

1)    Вычислим вероятность получения студентом отметки «2». Для этого нужно разделить количество двоек на общее количество студентов. В результате получим:


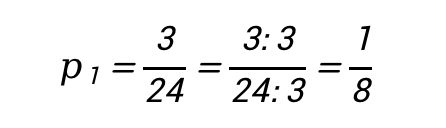
A number with numbers and linesDescription automatically generated with medium confidence

2)     Теперь вычислим вероятность получения студентом отметки «3». В результате получим:


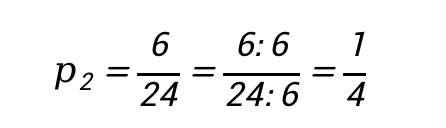
A number and numbers on a white backgroundDescription automatically generated

3)  Вычислим вероятность получения студентом отметки «4». В результате получим:


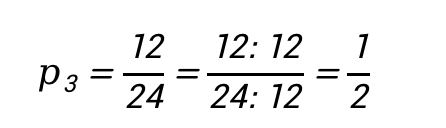
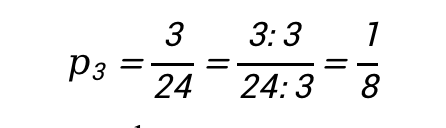
A number with numbers and linesDescription automatically generated with medium confidence

  1. Вычислим вероятность получения студентом отметки «5». В результате получим:


A number with numbers and linesDescription automatically generated with medium confidence

  1. Вычислим количество информации, которое содержит сообщение об отметке любого студента данной группы с помощью формулы (4).

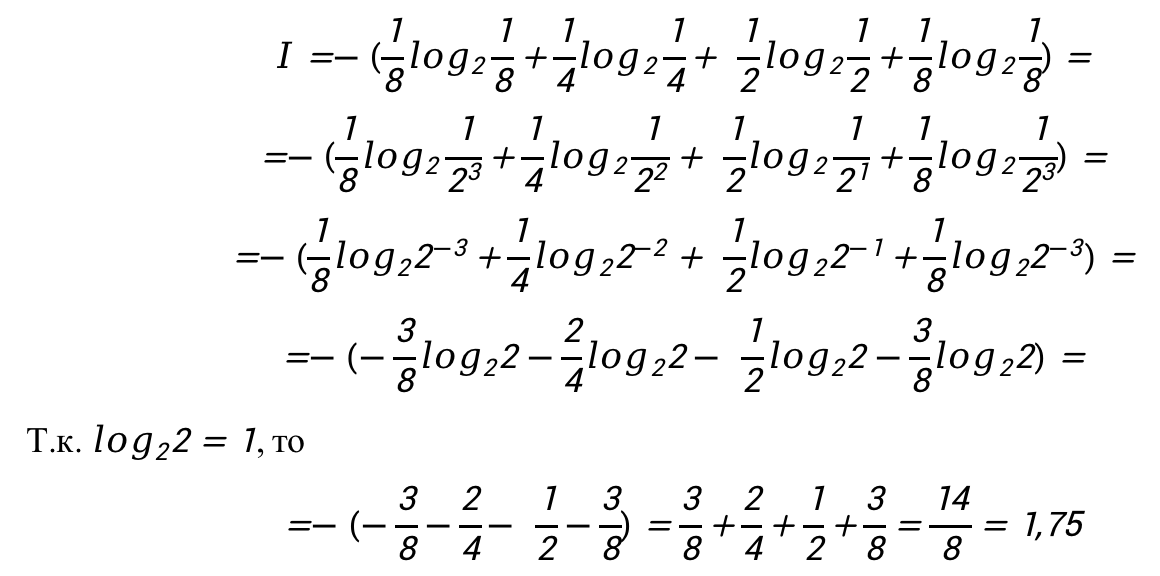
A math problem with numbers and equationsDescription automatically generated

Ответ: 1,75 бита

Задача 2. В пенале находятся желтые и красные карандаши в количестве 24 штуки. Сообщение о том, что из пенала достали желтый карандаш несет 2 бита информации. Определить число желтых и красных карандашей в пенале.

Решение

  1. Обозначим за х количество карандашей в пенале. Тогда воспользуемся формулой (4) и вероятность того, что вынутый карандаш окажется желтым:

 


 



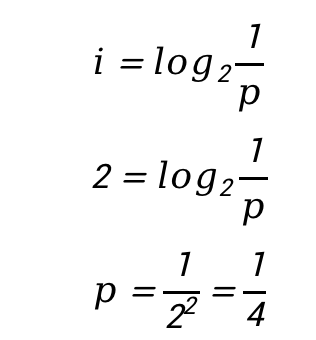
A group of math equationsDescription automatically generated

  1. Составим отношение и найдем х:




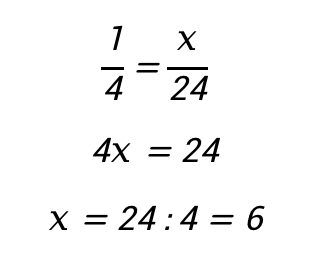
A math equations with numbersDescription automatically generated

Получили 6 желтых карандашей.

  1. Найдем количество красных карандашей. Для этого из общего количества карандашей вычтем количество желтых карандашей. В результате получим: 

Ответ: 6 желтых карандашей и 18 красных карандашей.

 

Вопросы и задания для самоконтроля

  1. Что собой представляет процесс измерения информации? Как называется наименьшая единица измерения информации?
  2. В каком случае применяется формула Хартли?
  3. В каком случае применяется формула Шеннона?
  4. Сколько байтов содержится в 12405 битах?
  5. При вытаскивании из корзины произвольного шара было получено 3 бита информации. Сколько чисел содержится в данном алфавите?
  6. В пенале находятся синие и зеленые карандаши в количестве 36 штук. Сообщение о том, что из пенала достали синий карандаш несет 6 битов информации. Определить число синих и зеленых карандашей в пенале.