2-практикa

Тема практической работы: «Выполнение операции с разными системами счисления».

Цель: обучение операциям перевода из двоичной, восьмеричной и шестнадцатеричной систем счисления в десятичную и наоборот; арифметическим действиям в двоичной, восьмеричной и шестнадцатеричной систем счислениям.

Оборудование: интерактивная доска для демонстрации компьютера учителя.

Ход занятия:

Актуализация знаний

1. Что такое система счисления?
2. Какая система счисления используется на математике?
3. Какие действия можно производить с числами в десятичной системе счисления?

Изложение нового материала

Сегодня на занятии мы научимся осуществлять переводы из десятичной системы счисления в двоичную, восьмеричную, шестнадцатеричную и наоборот, а также производить арифметические операции над данными системами. 

Для начала вспомним, какие цифры могут использоваться в самых распространенных системах счисления, а именно, в двоичной, восьмеричной, десятичной и шестнадцатеричной.

 

 

Таблица 1 – Цифры, входящие в разные системы счисления

Название системы счисления	Входящие цифры	Примеры
Двоичная	0, 1	101112; 11,1012
Восьмеричная	0, 1, 2, 3, 4, 5, 6, 7	2358; 12,78
Десятичная	0, 1, 2, 3, 4, 5, 6, 7, 8, 9	92310; 189,510
Шестнадцатеричная	0, 1, 2, 3, 4, 5, 6, 7, 8, 9, A, B, C, D, E, F	12AC16; 35,F16

 

Подстрочным индексом рядом с числом пишется основание системы счисления. Наибольшая цифра, входящая в систему счисления на один меньше названия системы счисления. Например, если система счисления называется пятеричной, то самая большая цифра, которая будет в таком числе равна 4. Такая ситуация получается, что система счисления показывает количество цифр, которые могут входить в систему счисления, а 0 входит в расчет. Для пятеричной системы счисления это 5 цифр (0, 1, 2, 3 и 4). Данное правило работает и для других позиционных (число зависит от месторасположения цифры в нем) систем счисления.

Чтобы получить из целого числа в десятичной системе счисления число в любой системе счисления, нужно делить десятичное число на основание нужно системы счисления до тех пор, пока полученное число не войдет в новую систему счисления. В таком случае, чтобы перевести из десятичной системы в двоичную необходимо делить нужное число на 2 до тех пор, пока не останется остаток, равный 1.

Рассмотрим примеры получения из целого числа, записанного в десятичной системе счисления, число в двоичной, восьмеричной и шестнадцатеричной системах счисления.

Задание 1. Переведите число 63₁₀ из десятичной системы счисления в двоичную.

Решение

Будем делить сначала заданное, а затем и полученные числа на 2 до тех пор, пока не получим 1. Вот такой результат получим:

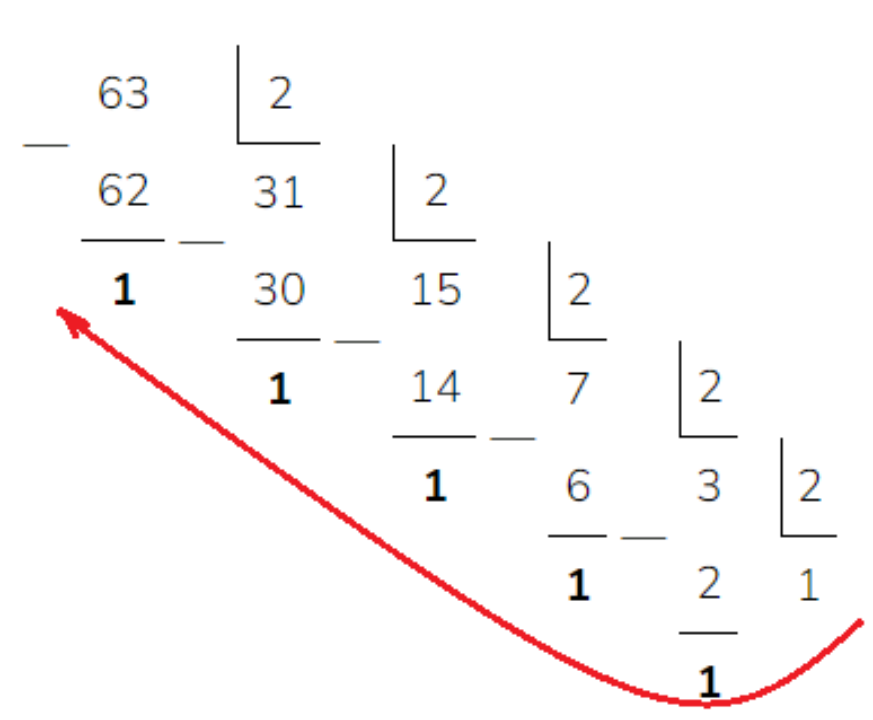
Ответ к данному задания нужно записывать в обратную сторону, т.е. с последнего полученного частного, а затем все остатки от деления в обратную сторону.

Ответ: 63₁₀ = 111111₂

Задание 2. Переведите число 127₁₀ из десятичной системы счисления в восьмеричную.

Решение 

Делим заданное число на 8 до тех пор, пока не получим число, входящее в восьмеричную систему счисления. Вот такой результат получим:

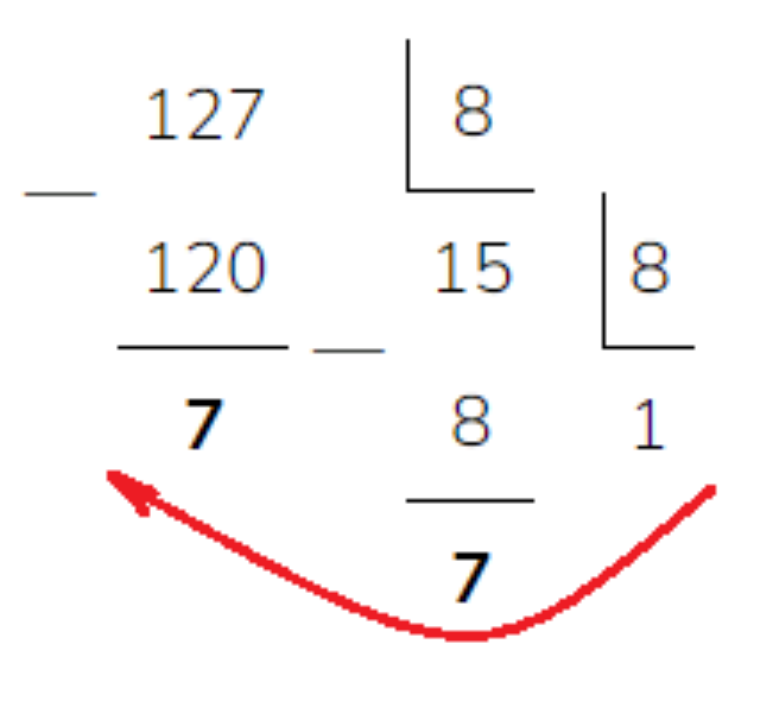
Ответ: 177₈

Задание 3. Переведите число 459₁₀ в шестнадцатеричную систему счисления.

Решение

Для перевода из целого числа из десятичной системы счисления в шестнадцатеричную необходимо делить заданное число на 16. При этом следует учесть, что если получим остаток равный 15, то нужно писать F, если 14 – то E, 13 – D, 12 – C, 11 – B, 10 – A. Вот такой результат получим

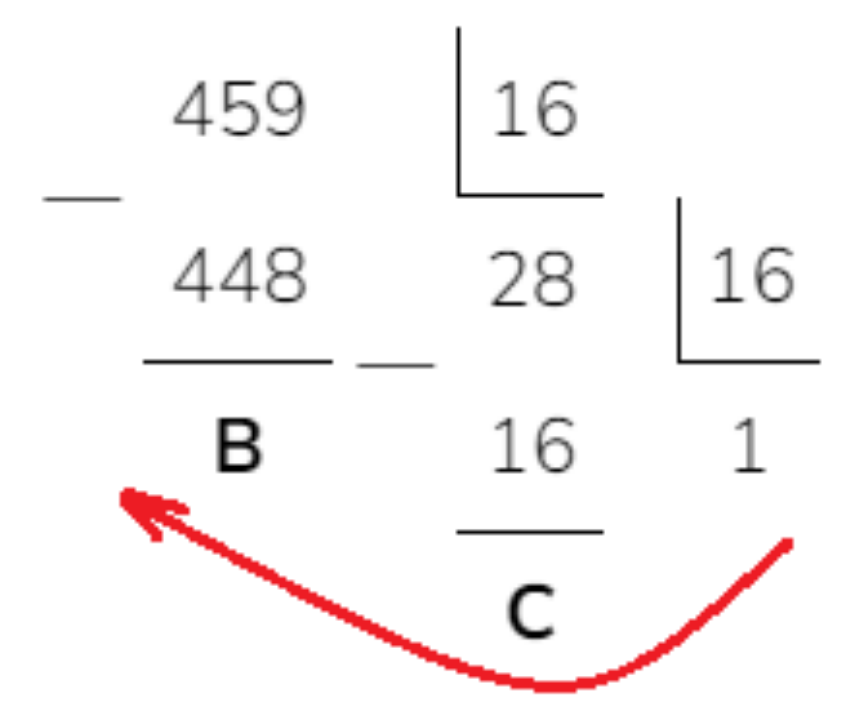
459 – 448 = 11, поэтому записали B.

28 – 16 = 12, поэтому записали С.

Ответ: 1СВ

Таким же образом можно перевести любое целое число в десятичной системе счиления в число любой другой системы счисления.

Рассмотрим возможности перевода из двоичной системы и восьмеричной системы в десятичную.

Задание 1. Переведите целое двоичное число 1011₂ в десятичное.

Решение

Чтобы целое число перевести из любой системы счисления в десятичную необходимо выполнить следующие действия:

1. Расставить под числом разряды, начиная с 0.
2. Брать первую цифру исходного числа и умножать его на текущее основание системы счисление, возведенное в степень соответствующего разряду умножаемого числа.
3. Прибавить следующую цифру, умноженную на текущее основание системы счисление, возведенное в степень соответствующего разряду умножаемого числа.
4. Пункты 2 и 3 чередовать до тех пор, пока не закончатся разряды числа.

Выполним перевод:

^{3  2  1  0}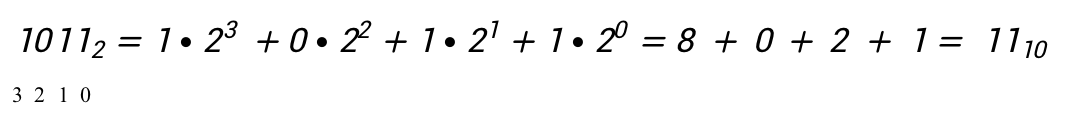

Ответ: 11₁₀

Задание 2. Переведите восьмеричное число 235₈ в десятичное.

Решение

Расставим разряды под восьмеричным числом и выполним перевод:

^{2  1  0}

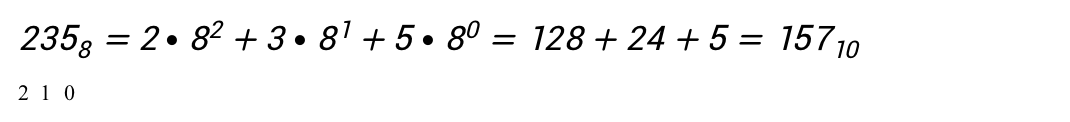
Ответ: 157₁₀

Таким же образом можно будет перевести целое число из любой системы счисления в десятичную.

Чтобы перевести из двоичной системы в восьмеричную или шестнадцатеричную можно сначала перевести из двоичной в десятичную, а только после этого из десятичной системы, путем деления на нужное основание, получить число в восьмеричной или шестнадцатеричной системе счисления.

Чтобы облегчить процесс перевода из двоичной системы счисления в восьмеричную можно воспользоваться следующей таблицей (Таблица 2):

 

Таблица 2 – Таблица перевода из двоичной системы счисления в восьмеричную и наоборот

Цифра в восьмеричной системе счисления	Двоичное представление	Цифра в восьмеричной системе счисления	Двоичное представление
0	000	4	100
1	001	5	101
2	010	6	110
3	011	7	111

 

Задача 1. Переведите число 10101111011₂ из двоичной системы в восьмеричную и шестнадцатеричную.

Решение

Чтобы перевести целое число из двоичной системы счисления в восьмеричную необходимо, двигаясь справа налево, отделять по три двоичных цифры. Если останется количество цифр меньше трех, то нужно будет поставить недостающее количество нулей слева. Результат будет выглядеть следующим образом:

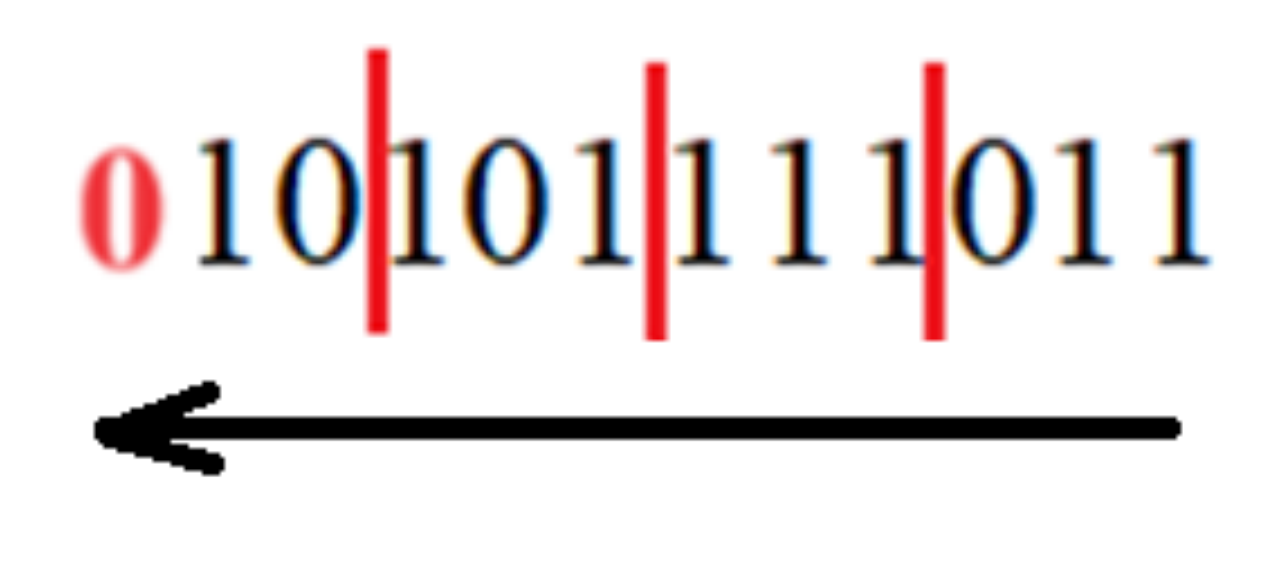
Опирясь на таблицу 2, определим какое восьмеричное число соотвествует триадам двоичной записи.

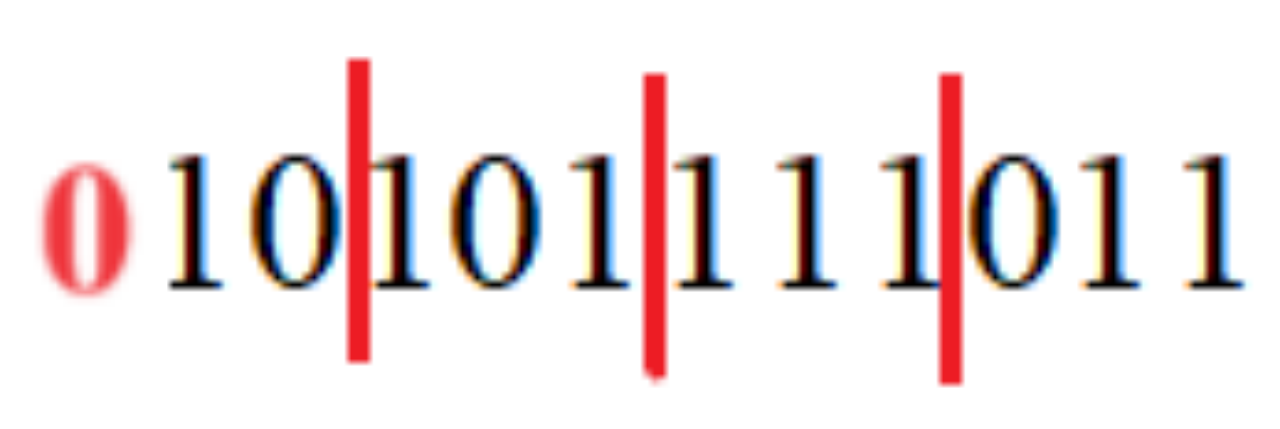
2     5        7      3

Запишем слева направо полученные числа в ответ.

Ответ: 2573₈

Задание 2. Переведите число 7123₈ из восьмеричной системы счисления в двоичную.

Решение

Для каждой цифры восьмеричного числа запишем соотвествующую двоичную триаду.

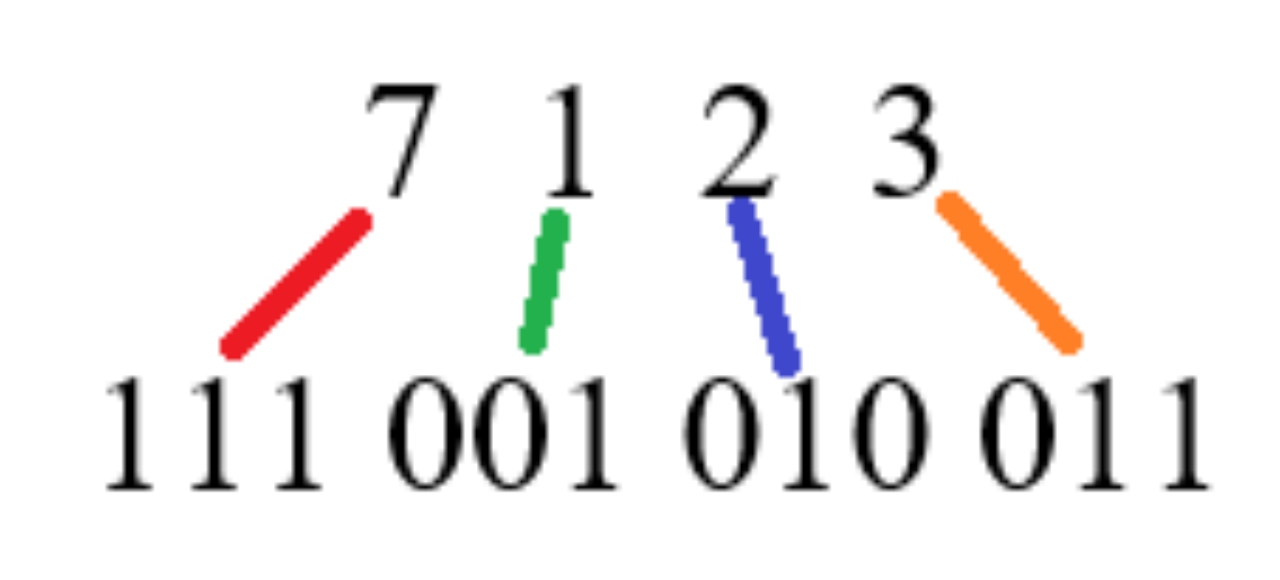
Запишем слева направо полученные числа в ответ.

Ответ: 111001010011₂

Чтобы облегчить процесс перевода из двоичной системы счисления в восьмеричную можно воспользоваться следующей таблицей (Таблица 3):

 

Таблица 3 – Таблица перевода из двоичной системы счисления в шестнадцатеричную и наоборот

Цифра в шестнадцатеричной системе счисления	Двоичное представление	Цифра в шестнадцатеричной системе счисления	Двоичное представление
0	0000	8	1000
1	0001	9	1001
2	0010	A	1010
3	0011	B	1011
4	0100	C	1100
5	0101	D	1101
6	0110	E	1110
7	0111	F	1111

 

Задание 1. Переведите число 10111101110₂ из двоичной системы счисления в шестнадцатеричную.

Решение

Чтобы перевести целое число из двоичной системы счисления в шестнадцатеричную необходимо, двигаясь справа налево, отделять по четыре двоичных цифры. Если останется количество цифр меньше четырех, то нужно будет поставить недостающее количество нулей слева. Результат будет выглядеть следующим образом:

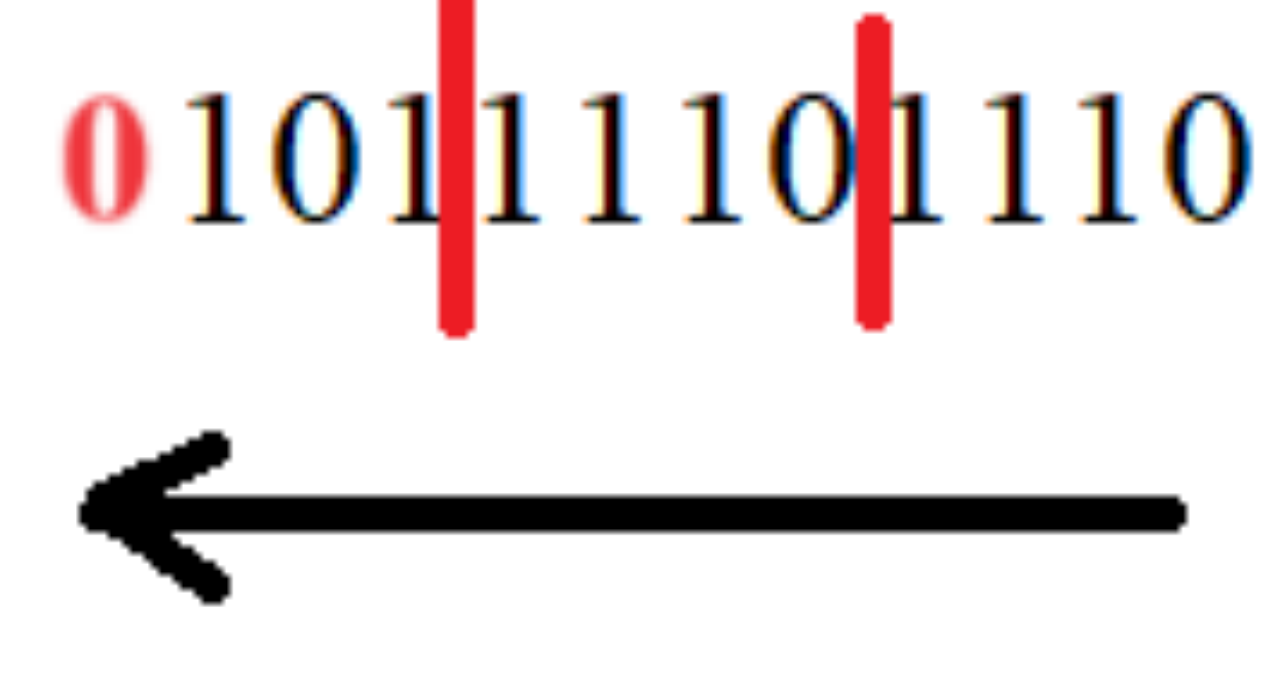
Опирясь на таблицу 3, определим какое шестнадцатеричное число соотвествует тетрадам двоичной записи.

  5         Е        Е

Запишем слева направо полученные числа в ответ.

Ответ: 5ЕЕ₁₆

Перевод чисел из шестнадцатеричной системы счисления в двоичную осуществляется также как и перевод из восьмеричной системы счисления в двоичную, но с применением таблицы 3.

Во всех позиционных системах счисления можно производить такие же арифметические операции, как и в десятичной ситеме счисления, а именно, складывать, вычитать, умножать и делить.

Задание 1. Сложить два целых числа 110110₂ и 1110₂ в двоичной системе счисления.

Решение

Чтобы сложить два числа необходимо записать их в столбик по принципу меньшее под большим, а далее произвести сложение, опираясь на правила поразрядного сложения:

0 + 0 = 0

0 + 1 = 1

1 + 0 = 1

1 + 1 = 10 (1 переходит в следующий более старший разряд)

В результате получим:

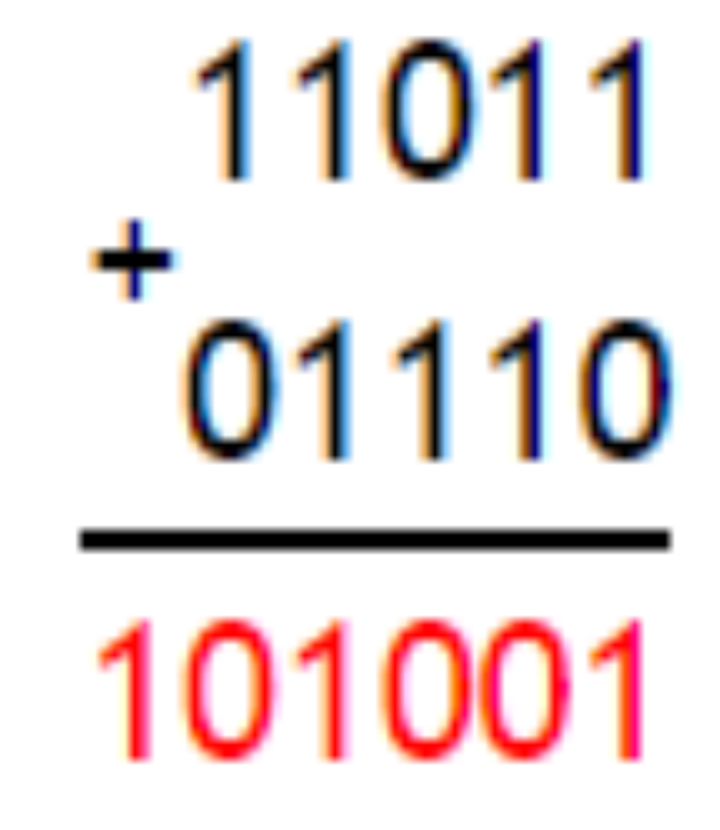
Ответ: 101001₂

Для других систем счисления сложение выглядит подобным образом

Задание 2. Сложить два числа 17₈ и 6₈

Решение

Чтобы сложить два числа в восьмеричной системе счисления необходимо расписать полученные числа на следующим образом:

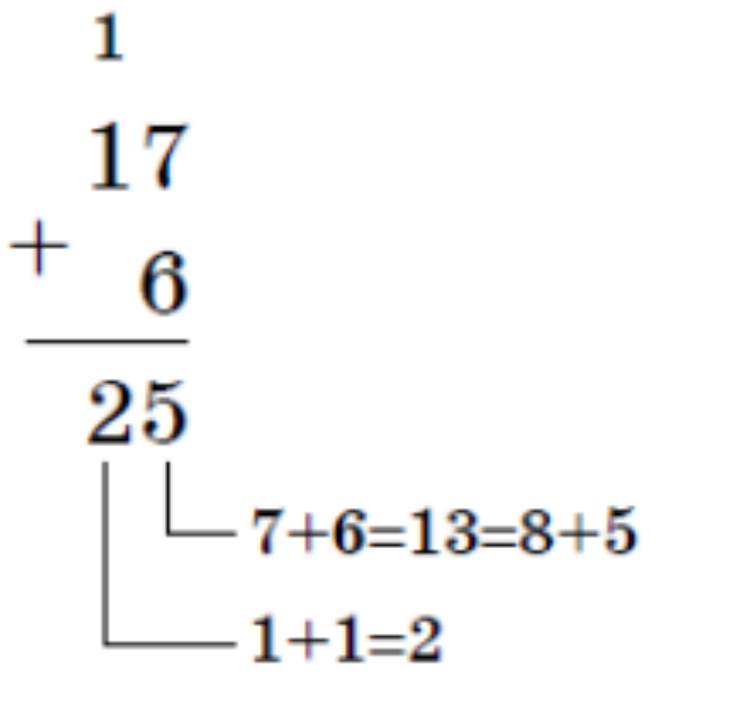
Ответ: 25₈

Задание 3. Найти разность двух двоичных чисел 10101₂ и 1011₂.

Решение

Чтобы найти разность двух двоичных чисел необходимо записать их в столбик по принципу меньшее под большим, а далее произвести вычитание, опираясь на правила поразрядного вычитания:

0 - 0 = 0

0 - 1 = 1 (занимаем 1 из страшего разряда)

1 - 0 = 1

1 - 1 = 10 

В результате получим:

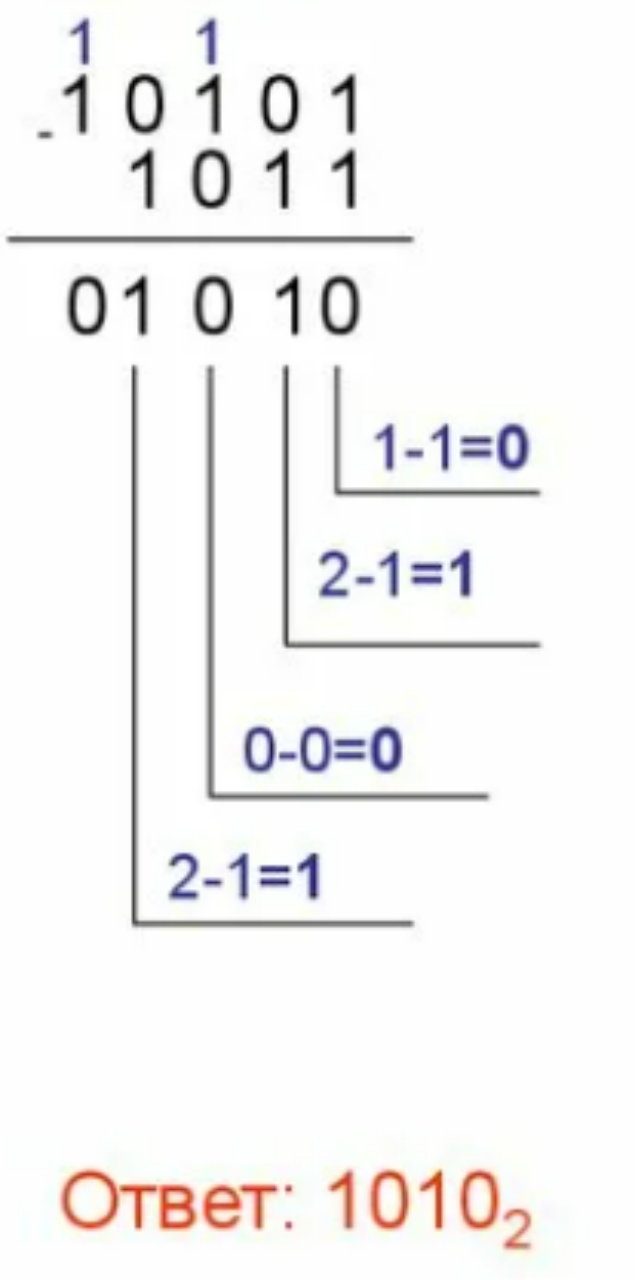
Ответ: 1010₂

Задание 4. Найти разность шестнадцатеричных чисел: С94₁₆ и 3ВС₁₆.

Решение

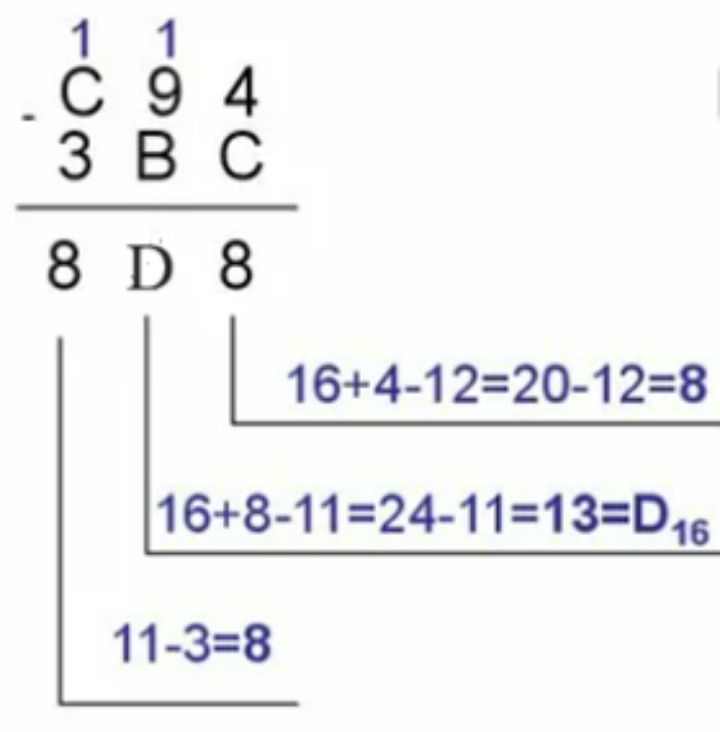
Ответ: 8D8₁₆

Задание 5. Выполните умножение двоичных чисел 11011₂ и 1101₂.

Решение

Произведем умножение каждой цифры первого множителя на каждую цифру второго множителя. Умножаем, используя таблицу поразрядного сложения:

0 * 0 = 0

0 * 1 = 0

1 * 0 = 0

1 * 1 = 1

А затем сложим:

Ответ: 101011111₂

Задание 6. Выполните умножение восьмеричных чисел 163₈ и 63₈.

Решение

Ответ: 13351₈

Задание 7. Выполните деление 100011₂ на 1110₂

Решение

Деление выполяется также как стандартное деление в столбик в десятичной системе счисления:

Ответ: 10,1₂

Задание 8. Выполните деление 13351₈ на 163₈.

Решение

Ответ: 63₈

 

Вопросы и задания для самоконтроля

1. Перечислите цифры, которые входят в восьмеричную систему счисления.
2. Переведите смешанное двоичное число из двоичной системы счисления в шестнадцатеричную и восьмеричную с помощью таблиц перевода.