3-практикa

Тема практической работы: «Информационно-логические основы персонального компьютера».

Цель: обучение вычислению логических функций и построению логических схем.

Оборудование: электронные таблицы Excel, графический редактор Paint, интерактивная доска для демонстрации компьютера учителя.

Ход занятия:

Актуализация знаний

1. Что такое высказывание в алгебре логики?
2. Какие высказывания называют простыми, а какие составными? Приведите по 2-3 примеры простых и составных высказываний.
3. Перечислите компоненты современного компьютера.

Изложение нового материала

На данном занятии мы рассмотрим, что собой представляют логические функции, каким образом их можно вычислить с помощью электронных таблиц и научимся стоить логические схемы для логичес

Логическими функциями являются правила преобразования входных логических данных в результат. К основным из них относятся: инверсия, конъюнкция, дизъюнкция. Результатом логической функции может быть 0 или 1.

Перед тем как приступить к рассмотрению основных логических функций и правил работы с ними повторим правила построения таблиц истинности:

1. У каждой таблицы, в том числе и таблицы истинности, должен быть заголовок.
2. В шапке таблицы необходимо сначала перечислить все переменные, используемые в логическом выражении (причем необходимо писать переменные без отрицания даже, если используются только переменные с отрицанием). Затем записываются все переменные с отрицанием, если такие есть. После записываются выражения по действиям. Последнее действие можно не писать, а писать вместо него F (понимается как результат функции).
3. Количество строк в таблице истинности определяется по формуле 2ⁿ, где n – это количество переменных.
4. После того как названия всех столбцов написаны и определено количество строк можно используя формулы, вычислить результаты применения всех необходимых логических операций.

Инверсия – операция логического отрицания, заменяющее исходное значение на противоположное. В электронных таблица записывается «НЕ».

Задание 1. Постройте таблицу истинности для инверсии.

Запустим Excel, назовем Лист1 «Инверсия», а затем в ячейке А1 напишем название таблицы «Таблица истинности для инверсии». В ячейке А3 напишем «А», а в ячейке B3 напишем «не А». Т.к. переменная А может принимать только значения 0 или 1, то в нашей таблице будет две строки. В результате наша заготовка будет иметь следующий вид:

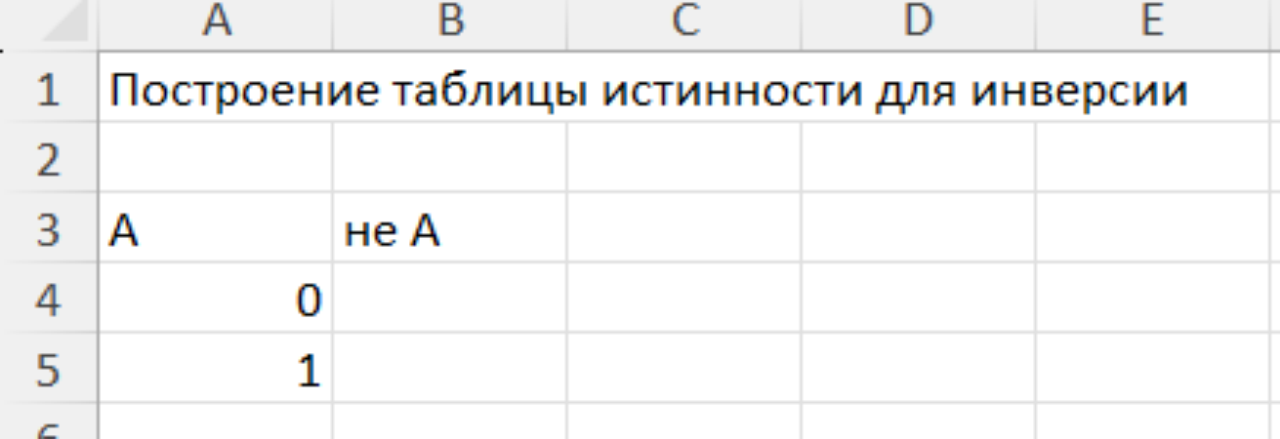
Рисунок 1 – Набросок таблицы для вычисления инверсии

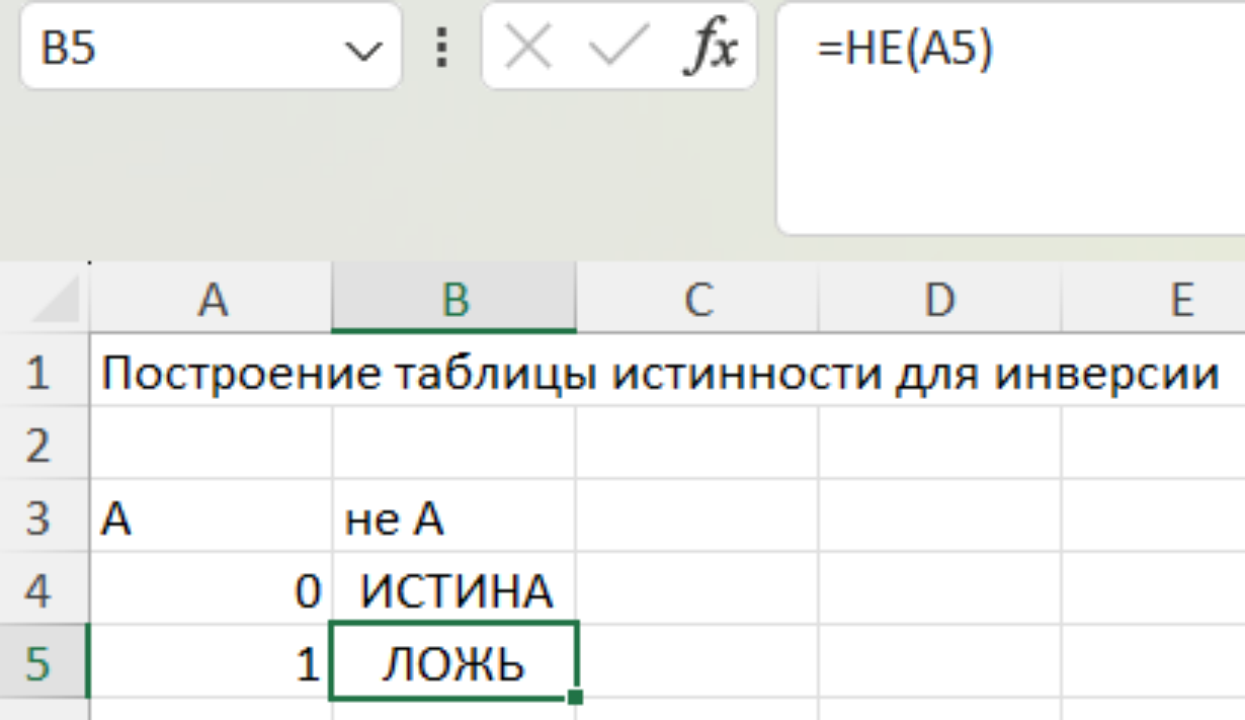
Вычислим результаты в столбце «не А». Для этого в ячейке В4 напишем «=НЕ» откроем скобку «(» и нажмем на ячейку А4. После этого закроем скобку «)» и нажмем Enter:

Теперь нажмем потянем за нижний правый угол ячейки В4 на одну ячейку вниз и получим значение в В5:

Оформим таблицу. Сделаем выделение границ. Для этого нужно выделить ячейки А3:В5 и на вкладке Главная выбрать Границы -> Все границы () и нажмем на выравнивание по центру ( ). После выделим ячейки А1:G1 и нажмем на кнопку Объединить и поместить в центре (). Выделим всю таблицe вместе с заголовком и сделаем шрифт Times New Roman, размер 14. Выделим заголовок и сделаем его по центру.

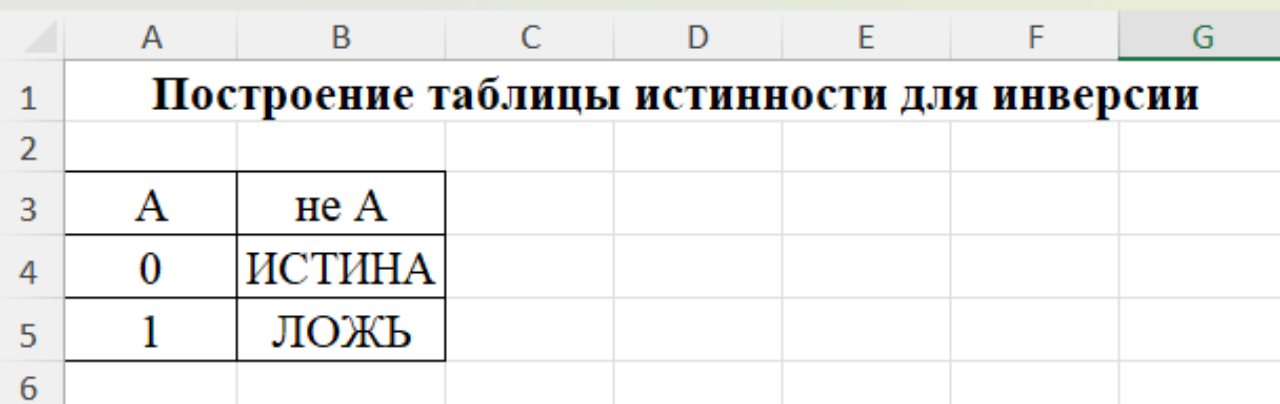
Рисунок 4 – Оформленное задание по инверсии

Конъюнкция – это операция логического умножения, которая истинна тогда и только тогда, когда значения всех переменных, входящих в выражение, являются истинными. В электронных таблица записывается «Н».

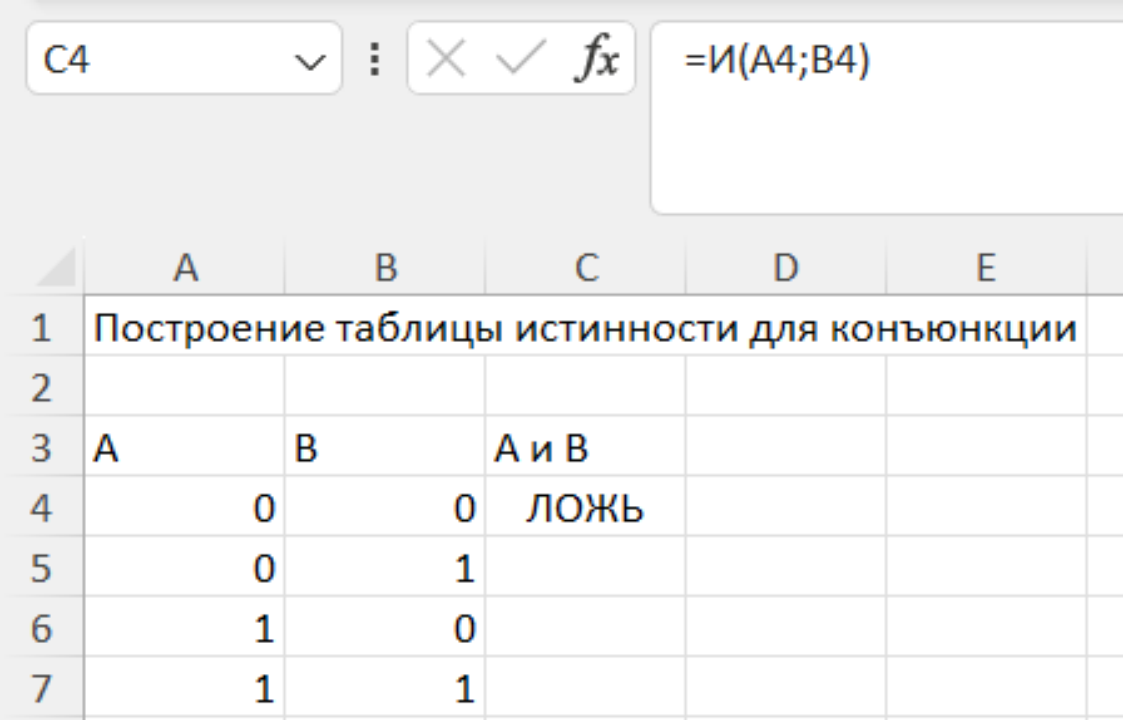
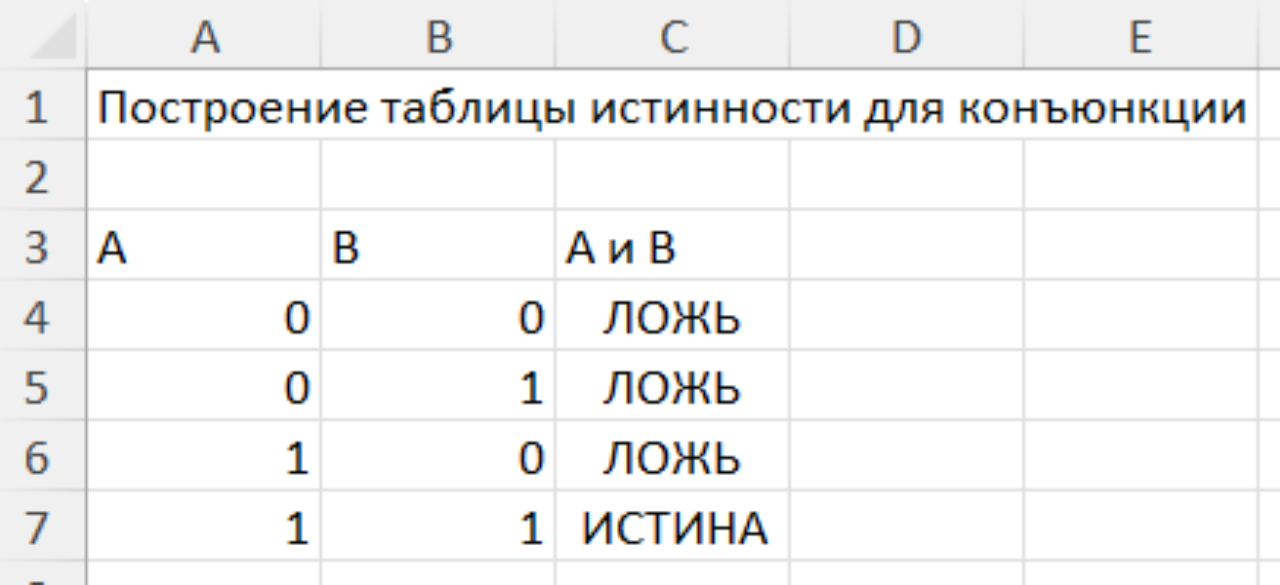
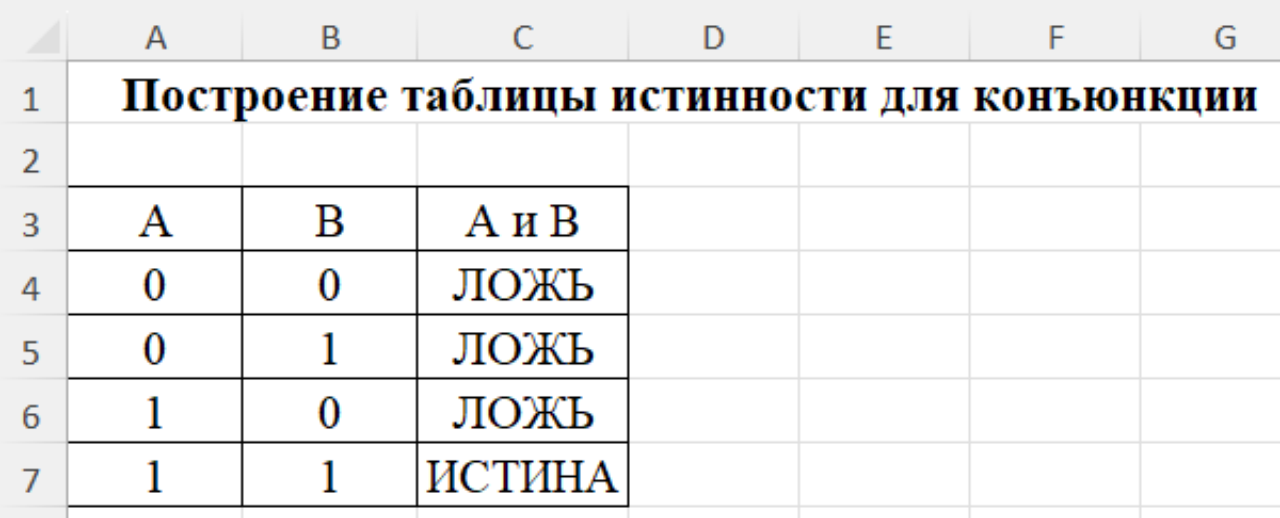
Задание 2. Постройте таблицу истинности для конъюнкции.

Решение

1. Создадим второй лист в файле Excel и назовем его «Конъюнкция».
2. Подготовим заготовку переменных и действий. Т.к. у нас операция логического умножения является составной, то в процессе должны участвовать две переменные, поэтому будет заполнено 2²=4 строки. Заполним входные наборы для переменных А и B, начиная с набора, состоящего из нулей и заканчивая набором, состоящим из единиц. В результате получим следующую ситуацию:
3. Выполним умножение в ячейке С4. Напишем в ней «=И», откроем скобку «(» нажмем на ячейку А4, поставим «;» и нажмем на В4. Затем закроем скобку «)» и нажмем Enter.
4. Протянем за уголок

1. Оформим как в предыдущем задании.

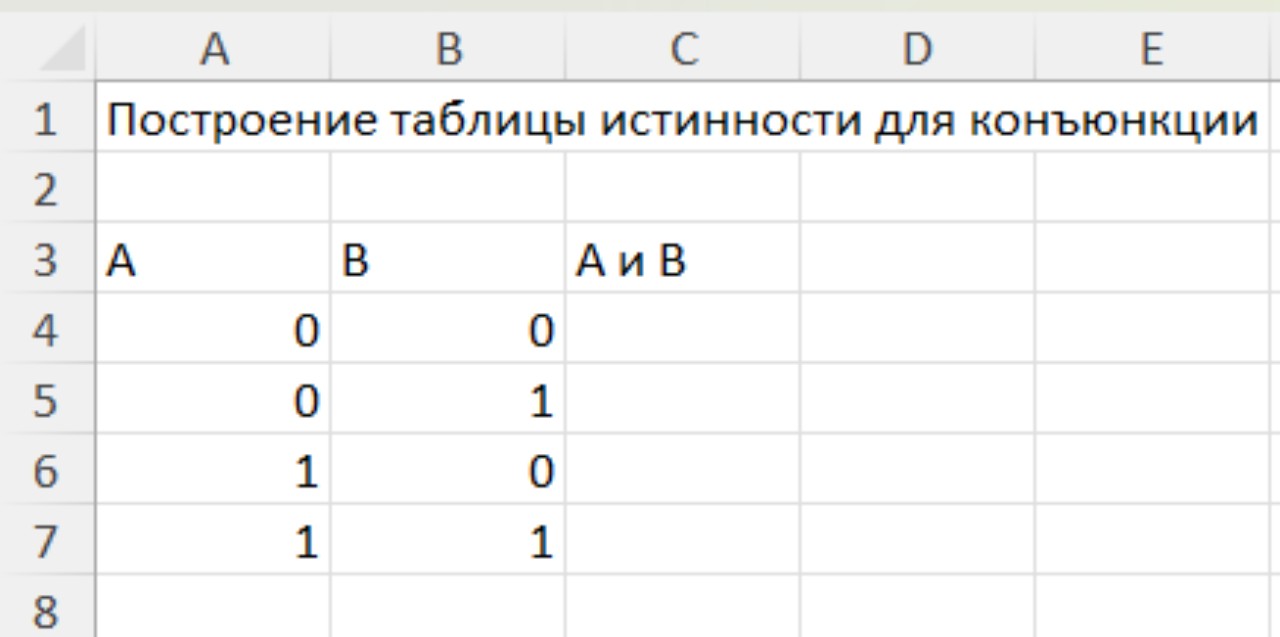
Дизъюнкция – это операция логического сложения, которая ложна тогда и только тогда, когда значения всех переменных, входящих в выражение, являются ложными. В электронных таблица записывается «ИЛИ».

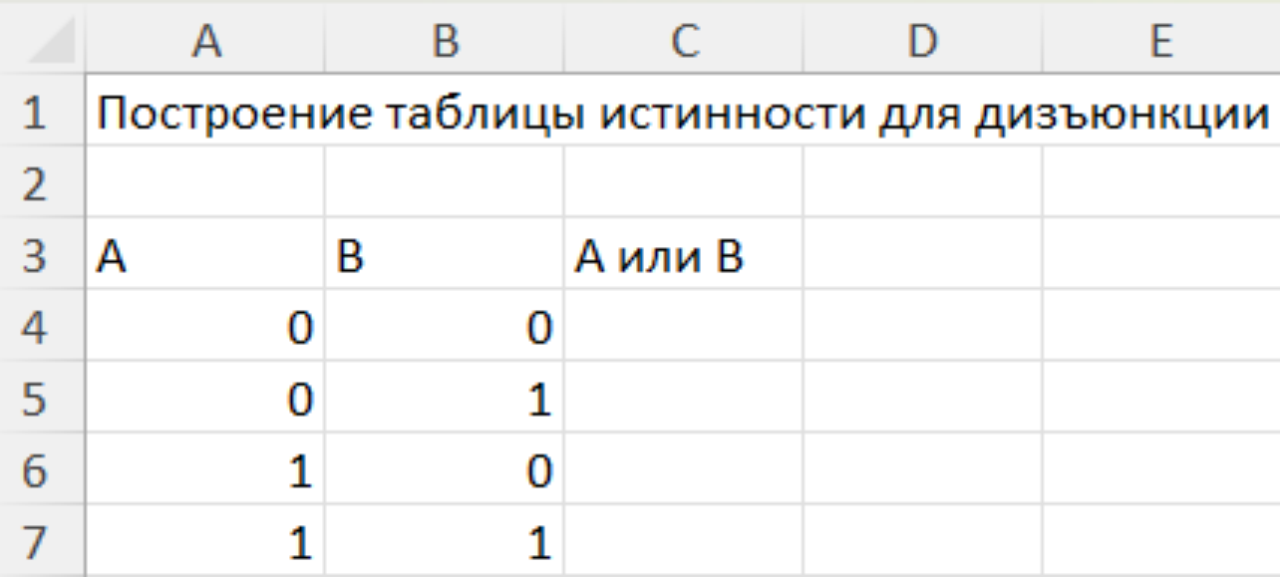
Задание 3. Постройте таблицу истинности для дизъюнкции.

Решение

1. Создадим третий лист в файле Excel и назовем его «Дизъюнкция».
2. Выполним те же действия, что и в пункте 2, но только вместо «И» пишем «ИЛИ».
3. Выполним сложение в ячейке С4. Напишем в ней «=ИЛИ», откроем скобку «(» нажмем на ячейку А4, поставим «;» и нажмем на В4. Затем закроем скобку «)» и нажмем Enter.

1. Протянем за уголок.
2. Оформим как в предыдущем задании.

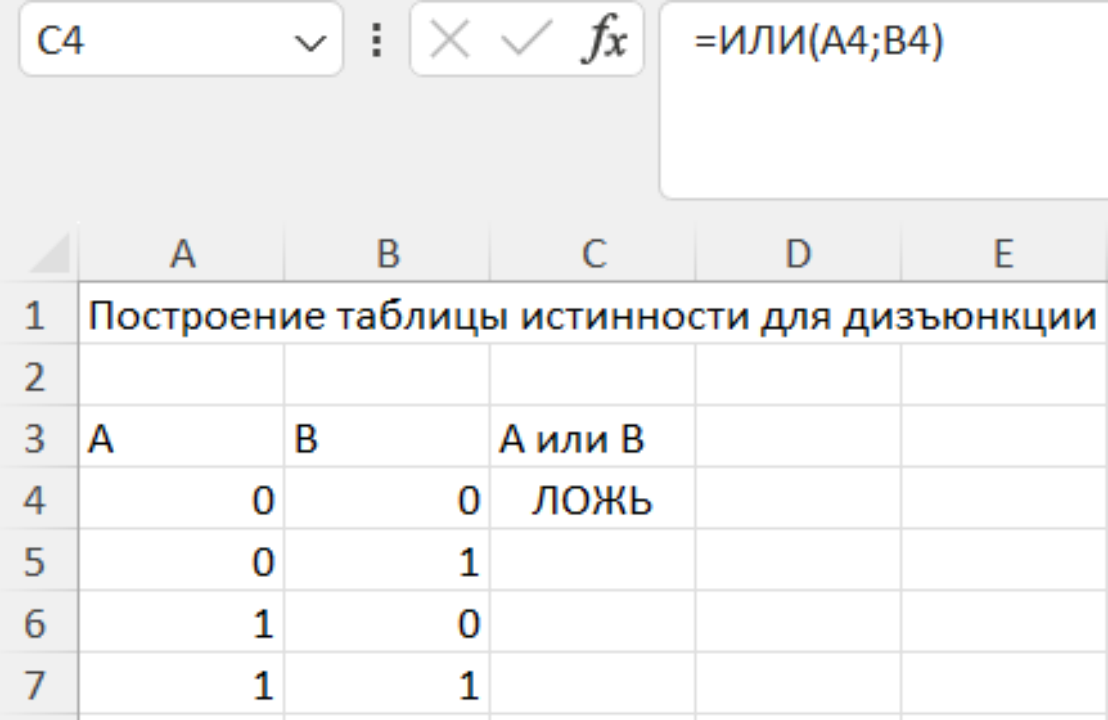
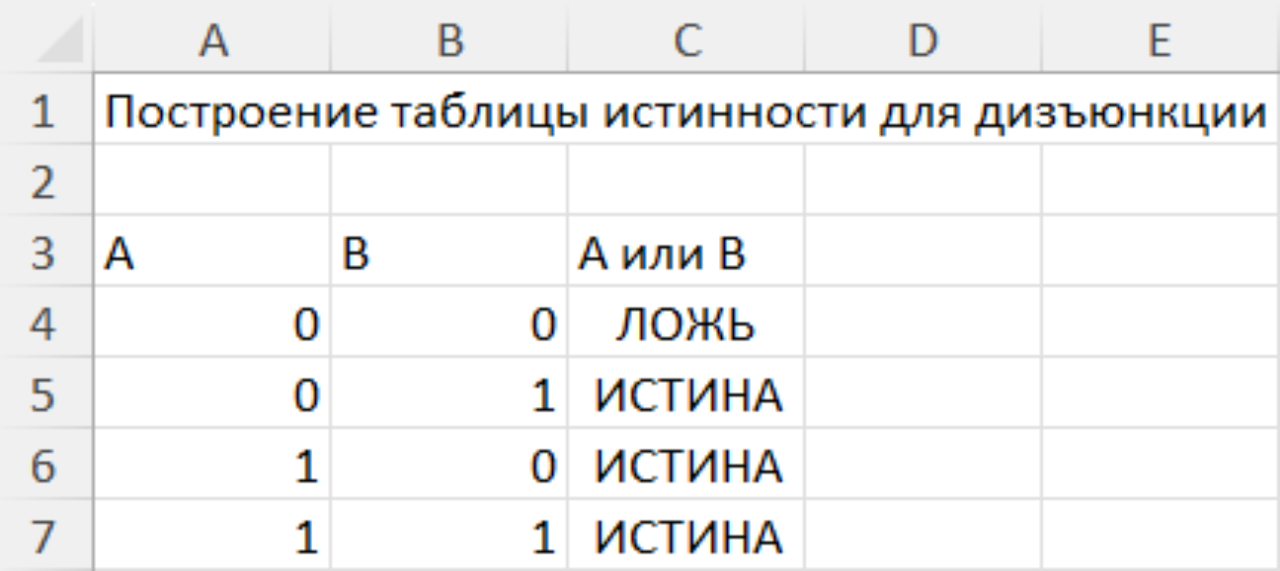
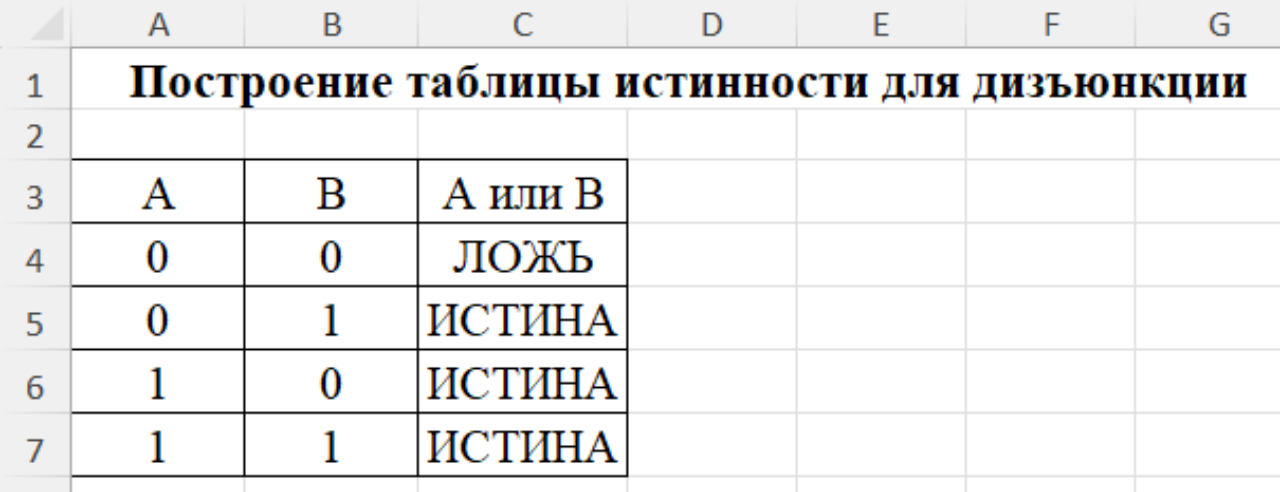
Сохраните файл под названием Таблицы_НЕ_И_ИЛИ.xlsx в папку со своей фамилией.

Приоритеты логических операций (от высшего к низшему):

1. Инверсия.
2. Конъюнкция.
3. Дизъюнкция.

Задание 4. С помощью построения таблицы найдите истинность следующего выражения .

В данном выражении с помощью алгебры логики записаны обозначения следующих символов:  - не,  - или,  - и.

Решение

1. Создайте файл Excel под названием Вычисление логического выражения.xlsx.
2. Построим заготовку таблицы истинности, опираясь на правило построения таблиц истинности. В результате получим следующую заготовку:
3. Получим результаты столбца не А, применив к ячейке D4 формулу =НЕ(А4), а затем протянув ее по ячейку D11.
4. Результаты столбца Е получим, применив к ячейке Е4 формулу =И(В4;С4). Затем протянем по ячейку Е11.
5. Вычислим результаты столбца F. Для этого сложим результаты столбца не А с результатами столбца В и С. В ячейке F4 напишем = ИЛИ(D4;E4).

1. Оформим как в прошлых заданиях

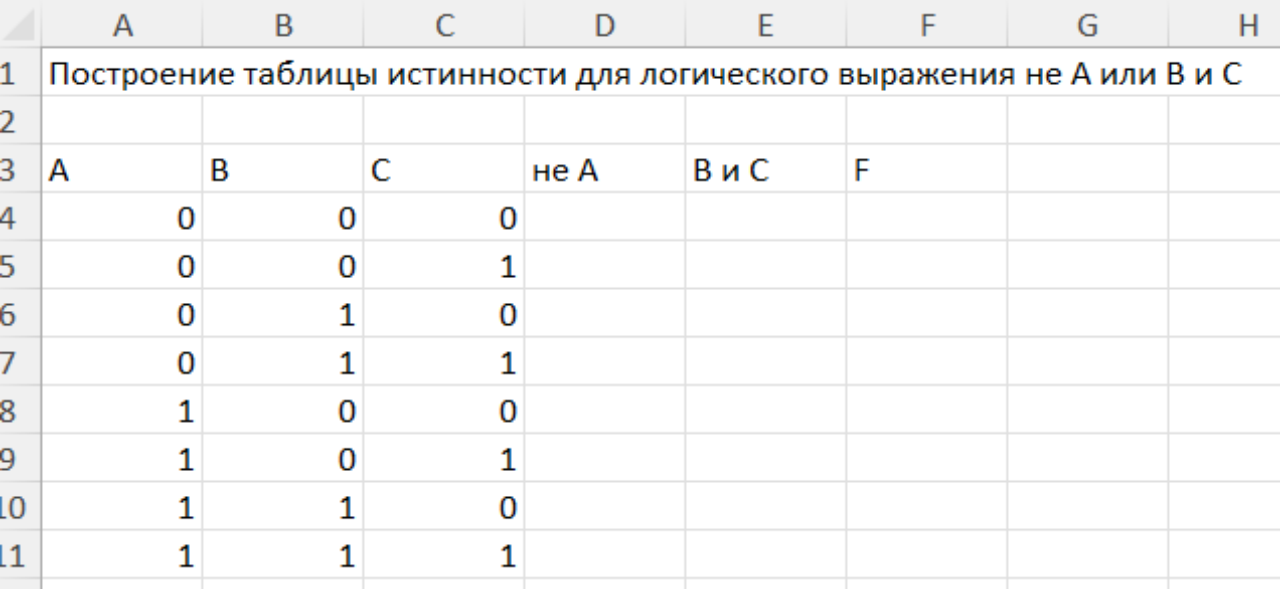
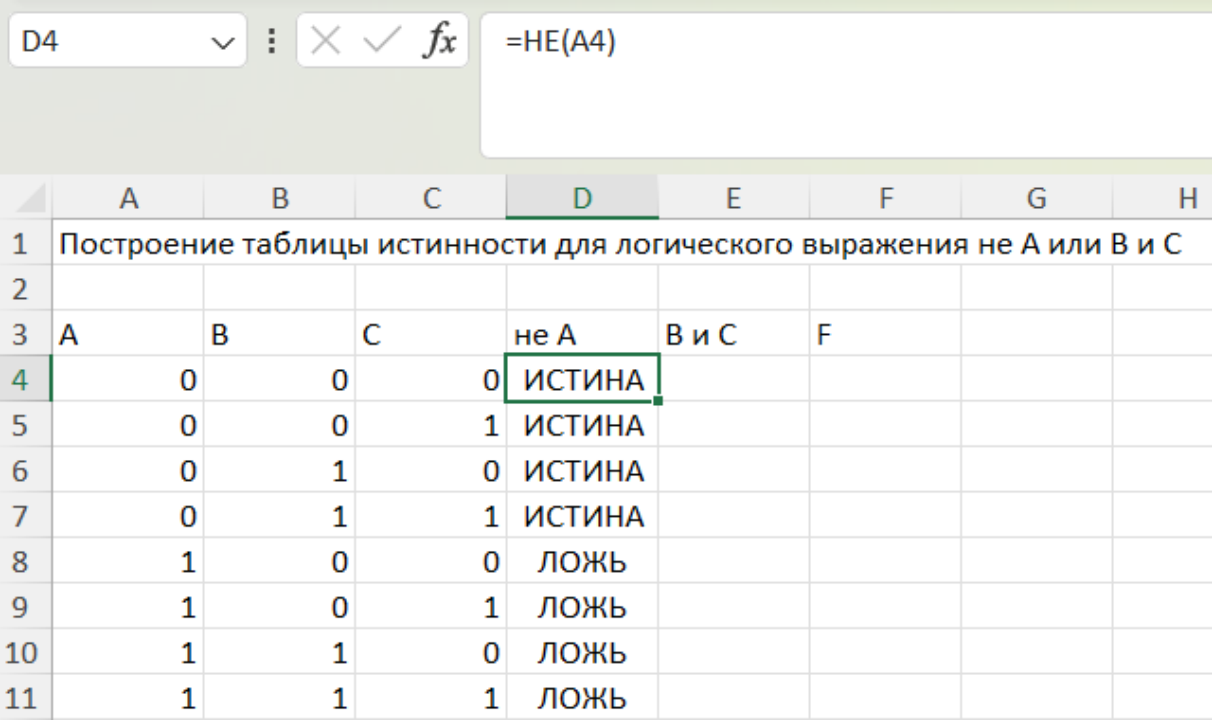
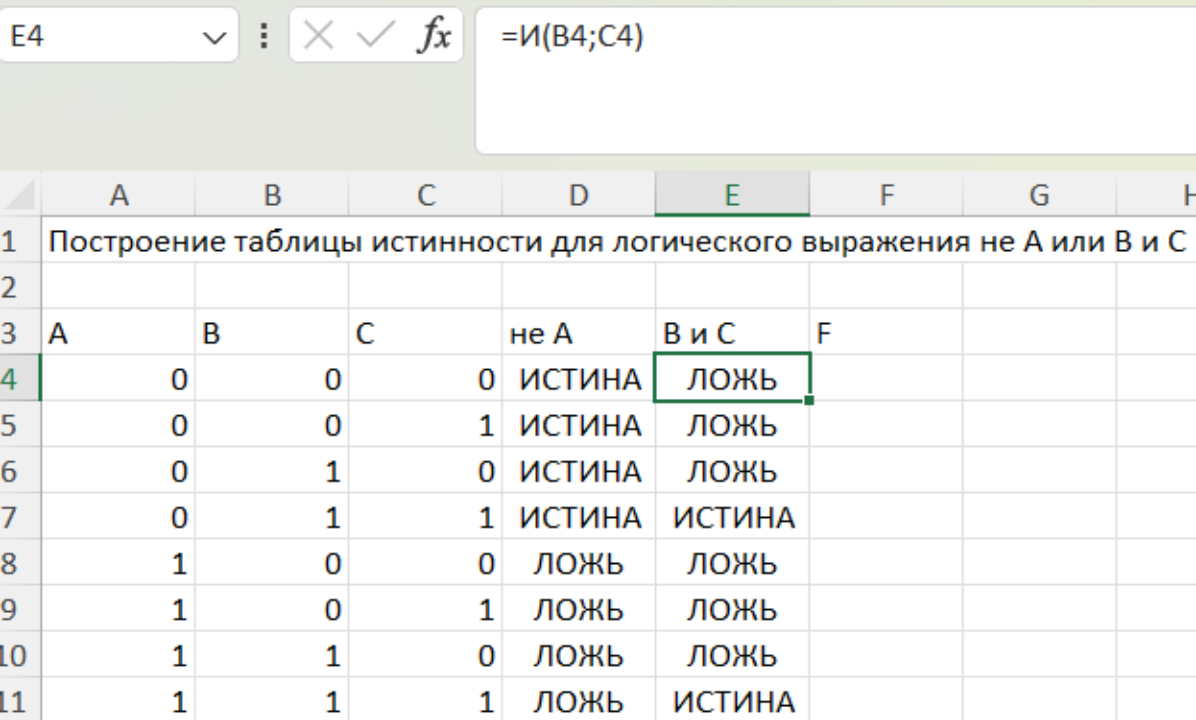
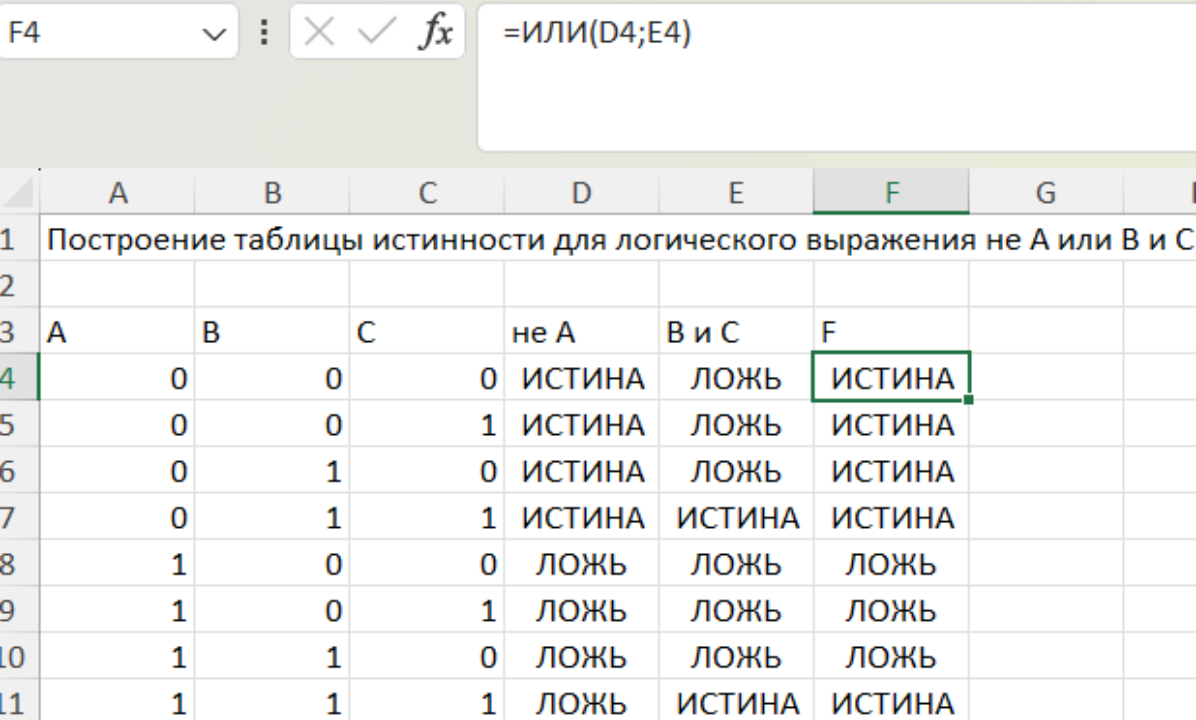
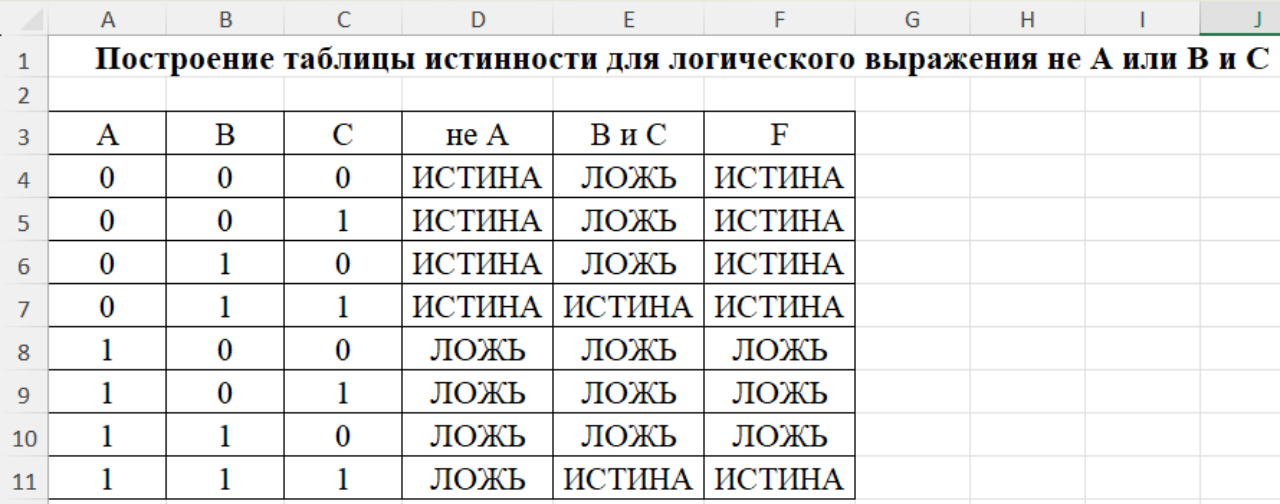
Сохраните файл в папке со своей фамилией.

К информационно-логическим основам компьютера относится построение схем логических элементов. Схемы логических элементов состоят из вентилей, к основным из которых относятся: инвентор, конъюнктор и дизъюнктор.

Инвентор – это вентиль, который отвечает за логическое отрицание. Он выглядит следующим образом:

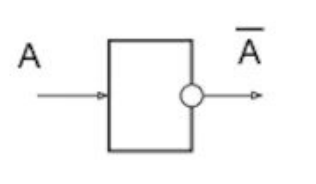
Конъюнктор – это вентиль, который отвечает за логическое умножение. Он выглядит следующим образом:

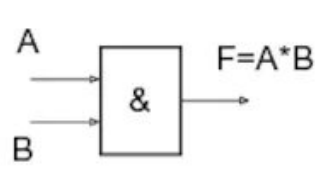
Дизъюнктор – это вентиль, который отвечает за логическое сложение. Он выглядит следующим образом:

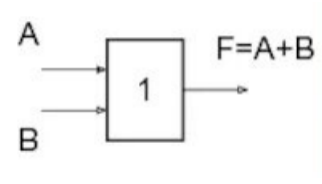
Задание 5. Постройте схему логического выражения .

Решение

Запустим графический редактор Paint и построим схему заданного логического выражения, используя представленные выше вентили

Вопросы и задания для самоконтроля

1. Что такое инверсия?
2. Что такое конъюнкция?
3. Что такое дизъюнкция?
4. С помощью таблицы истинности вычислите следующую логическую функцию: .
5. Постройте для выражения  логическую схему.